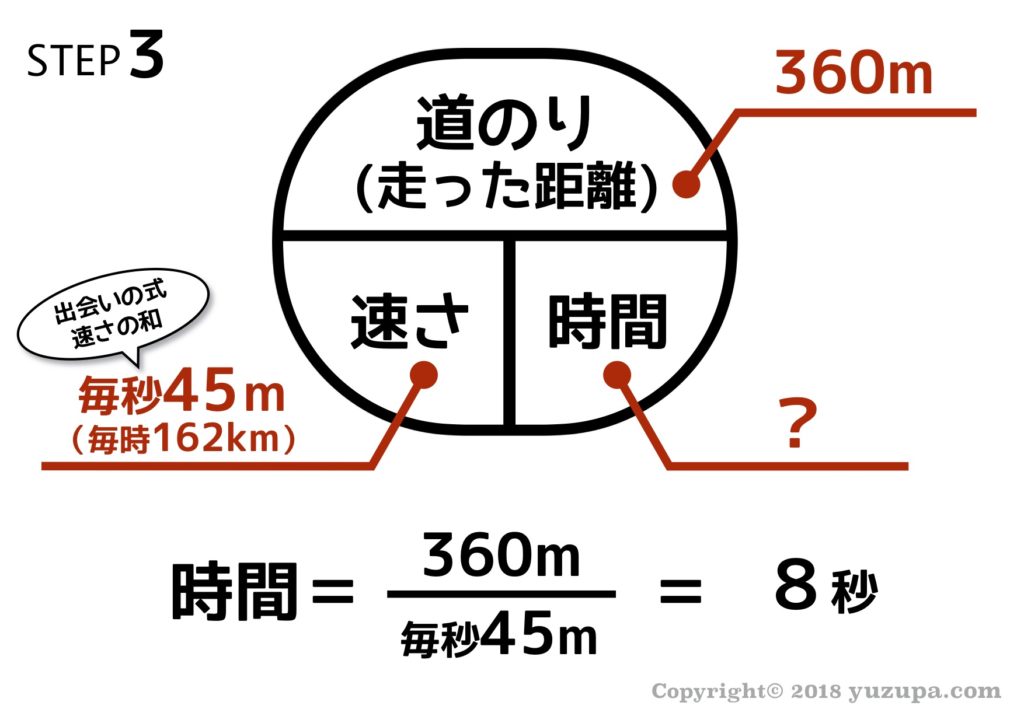
出会うまでの時間 = 360 ÷ (60 + 30) = 4になる。 答え:4分 旅人算の例 360m離れているAとBが向かい合って、Aが分速60m、Bが分速30mで歩きはじめたときの、出会うまでの時間は何分か? 500m離れているAとBが向かい合って、Aが分速30m、Bが分速70mで歩きはじめたときの、出会うまでの時間は何分か? 450m離れているAとBが向かい合って、Aが分速40m、Bが分速60mで歩きは
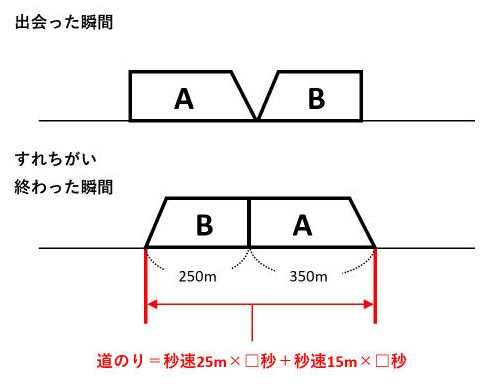
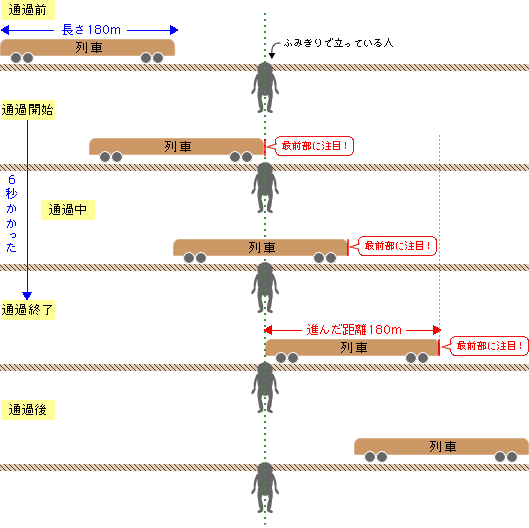
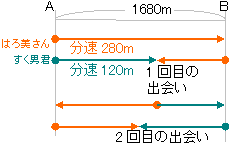
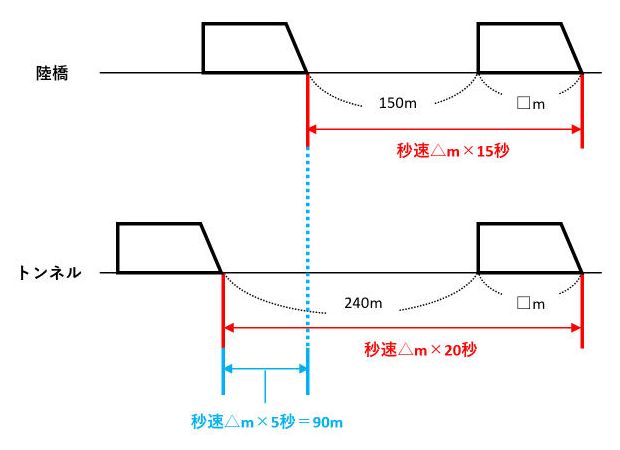
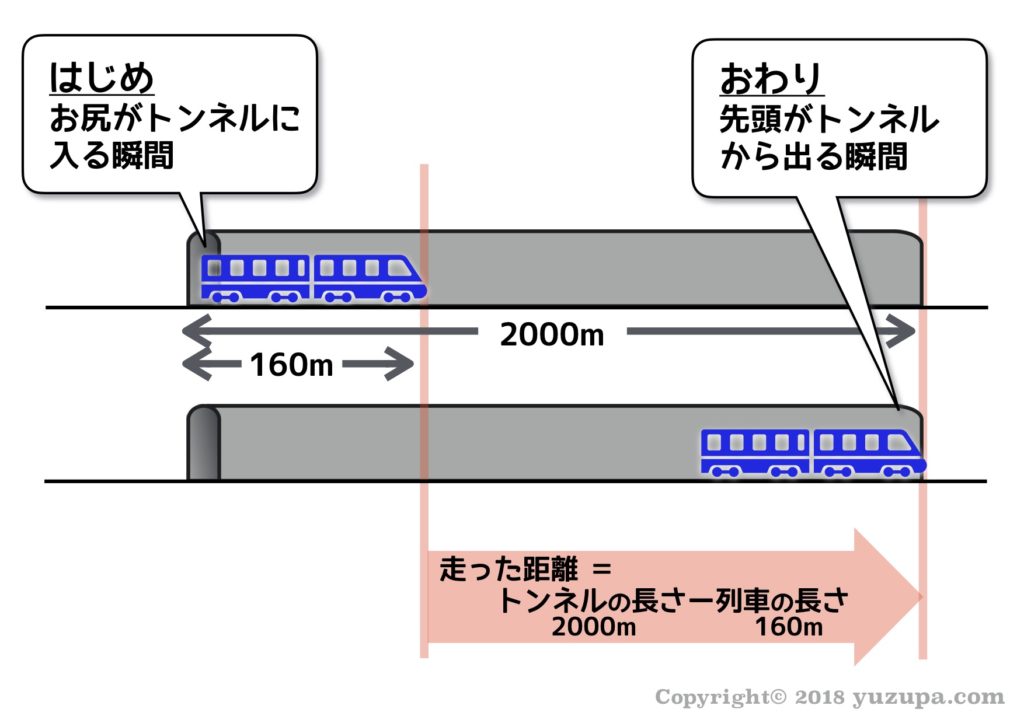
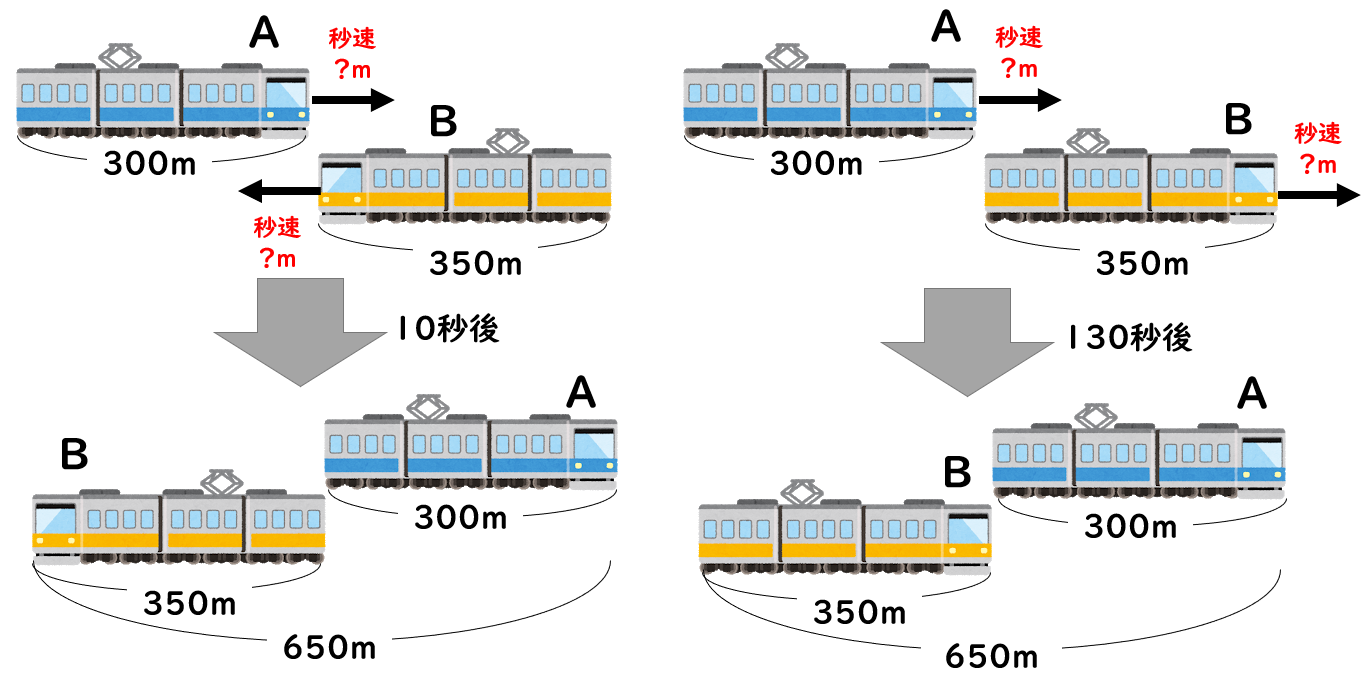
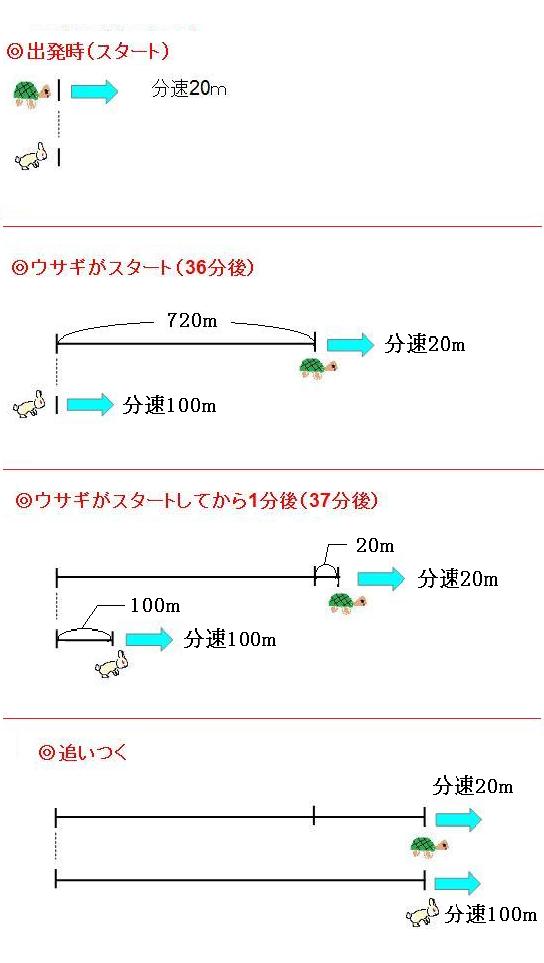
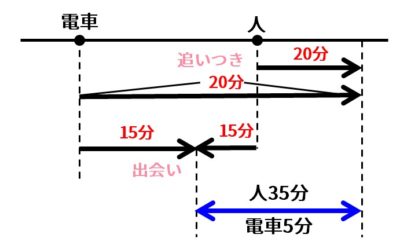
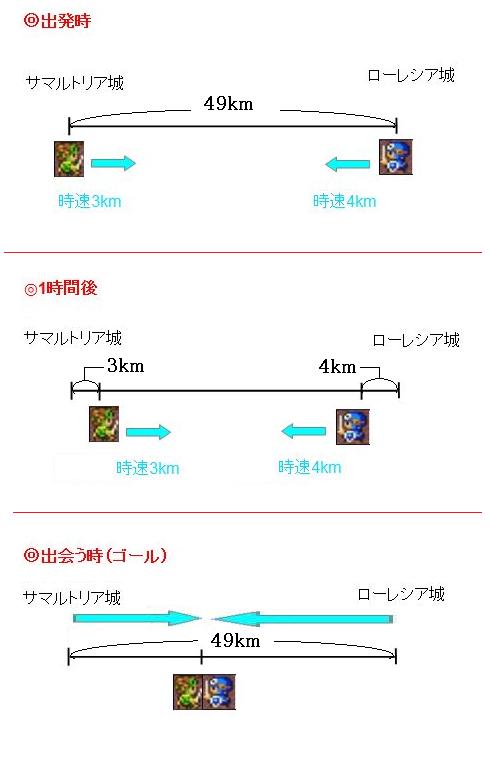
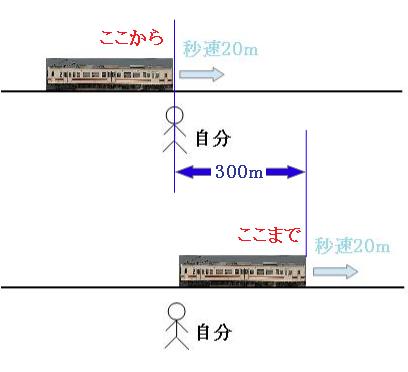
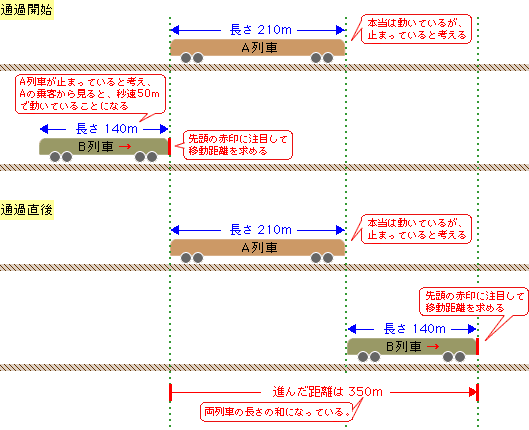
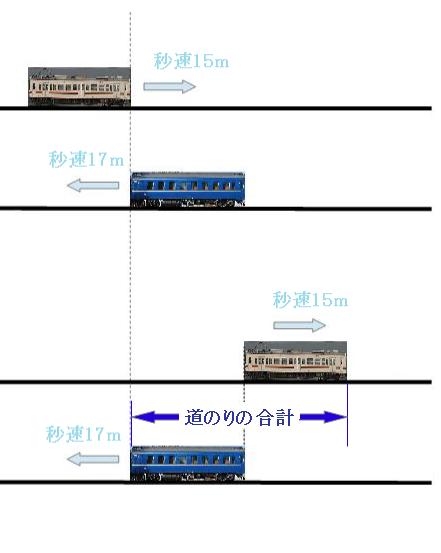
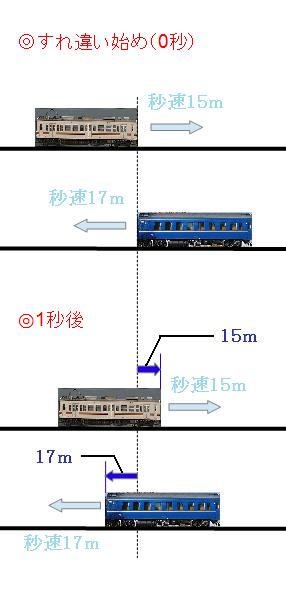
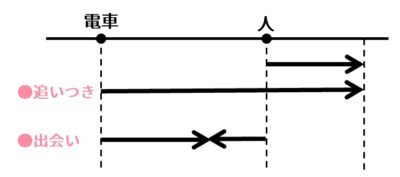
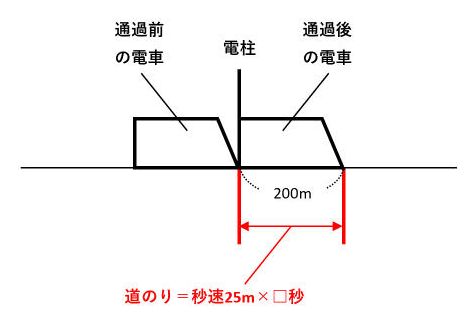
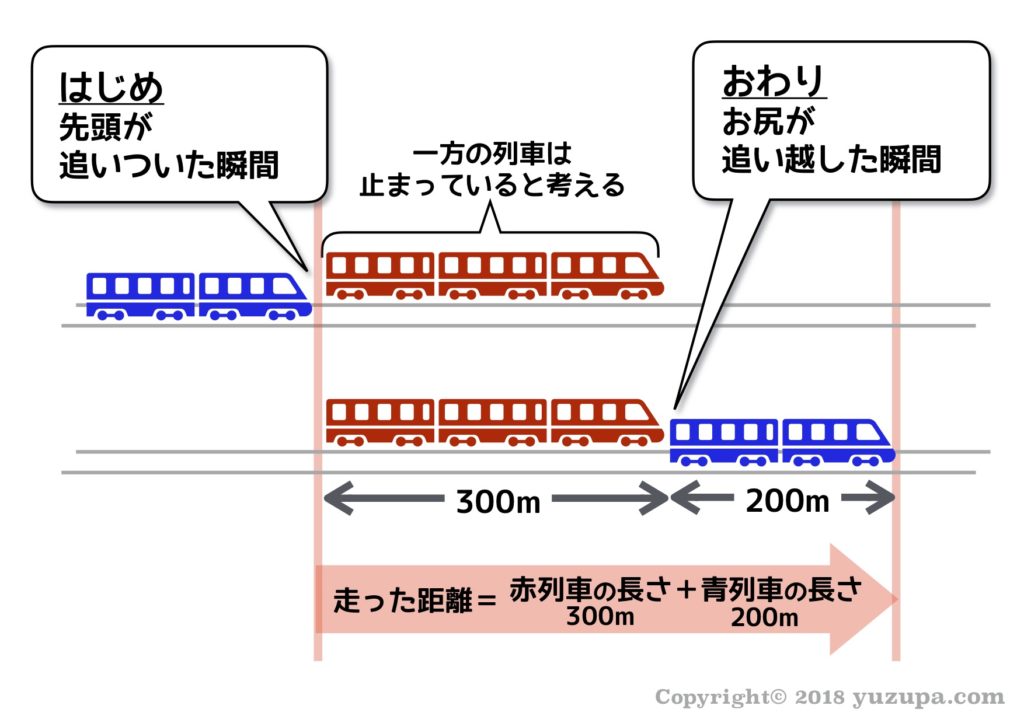
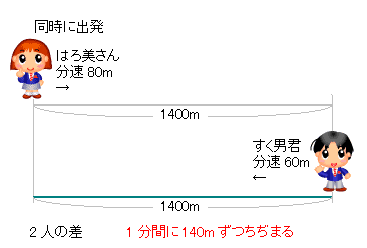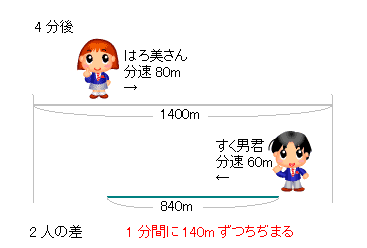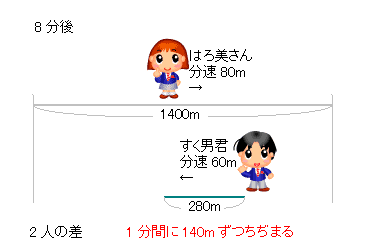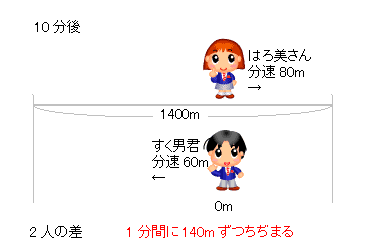
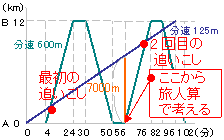
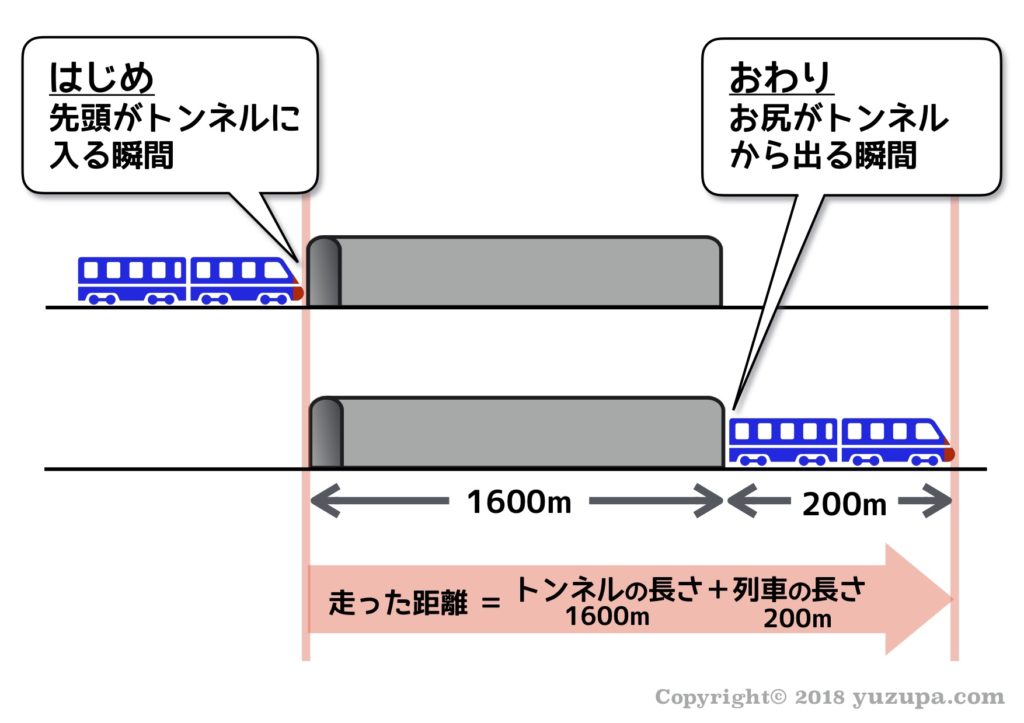
出会い算 電車-「電車同士の通過」のパターンです。 「すれ違い」なので、「出会い算」の考え方になります。 t字のイメージを活用しながら、 「は・じ・き」の情報を埋めていきます。 「速さ(は)」は、 「出会い算」なので、足し算になります。22/6/19 そこで、 1 1 分間が経過しました。 すると、女の人は分速 80 80 (m)、旅人は分速 60 60 (m)で進むので、二人で合わせて 80 60 = 140 80 60 = 140 (m)進んだことになります。 よって、二人の間のキョリも、 4 − 140 = 280 4 − 140 = 280 (m)まで縮まります。 したがって、 1 1 分経過するごとに 140 140 (m)キョリが縮まるので、 4 ÷ 140 = 3 ( 分) 4 ÷ 140 = 3 ( 分) つま
出会い算 電車のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  |  |
「出会い算 電車」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「出会い算 電車」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「出会い算 電車」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  |  |
「出会い算 電車」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「出会い算 電車」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「出会い算 電車」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「出会い算 電車」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「出会い算 電車」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
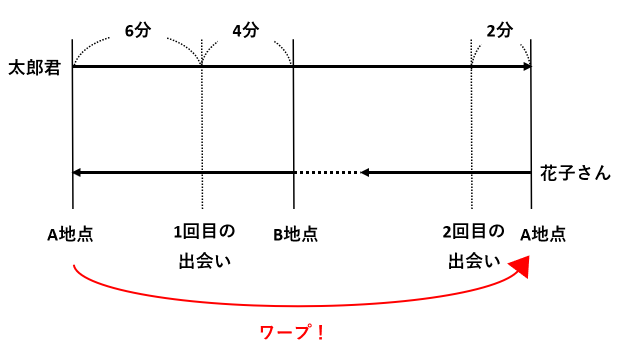
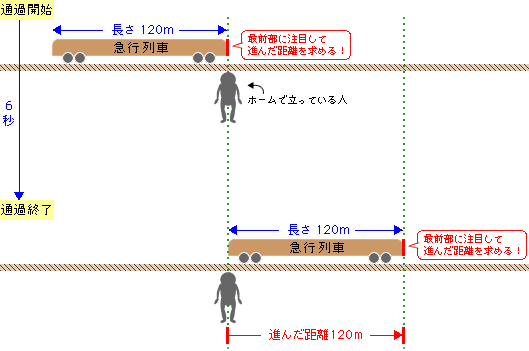
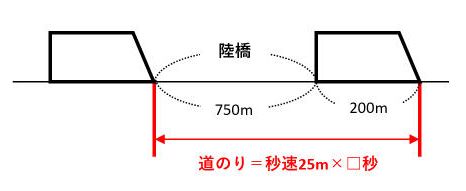
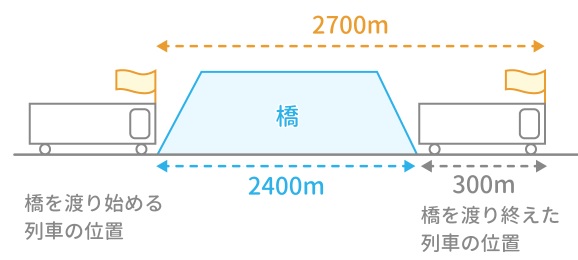
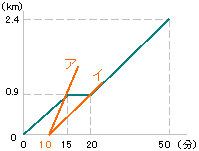
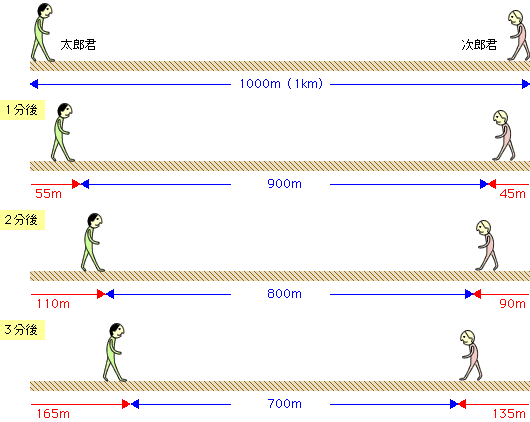
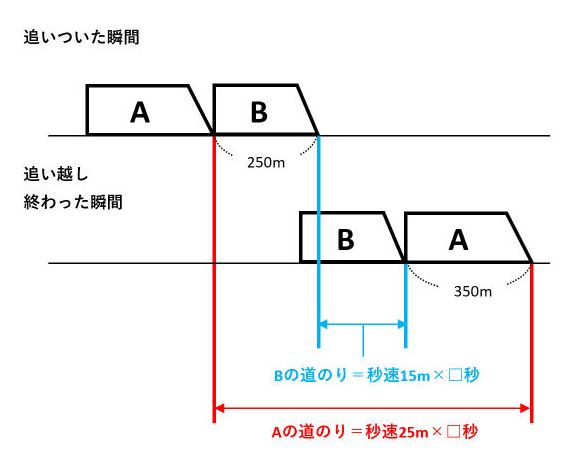
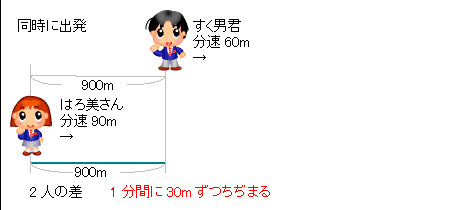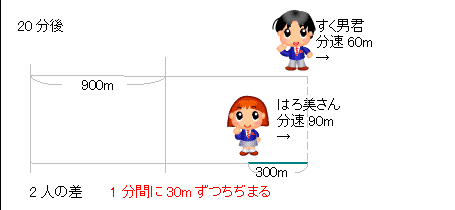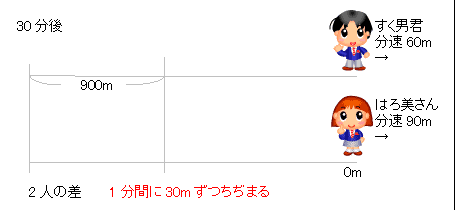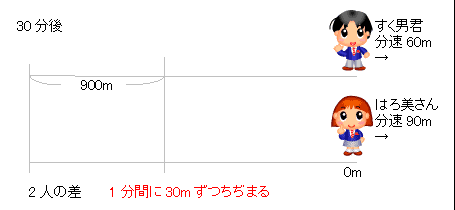
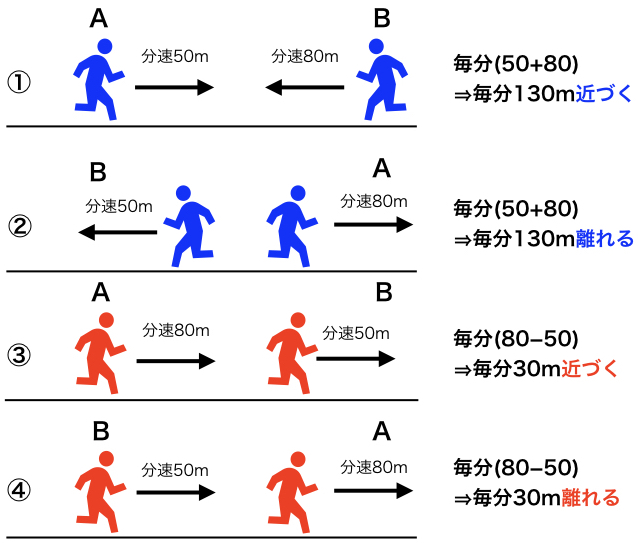
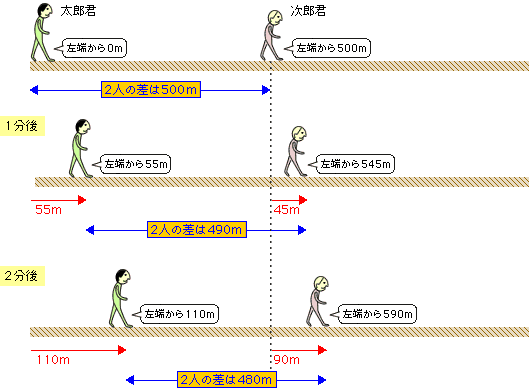
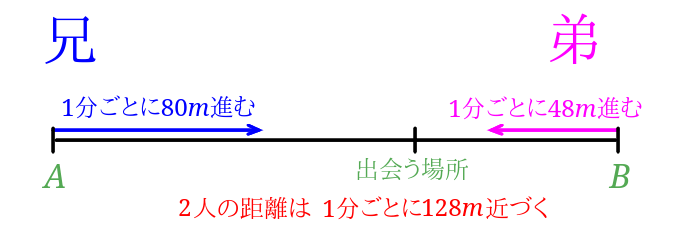
旅人算の中で基本となる 出会い算 について考え方と解き方のポイントを解説します。 出会い算とは、同時または時間差で反対方向に出発した2人が出会うまでの時間や距離を求める問題です。 出会い算の 基本問題 は次のような問題です。 出合い算(旅人算)の基本問題 駅から自宅に向かってお父さんが分速80mで歩き、自宅から駅に向かって和治さんが分速60mこれは公式にあてはめて解くことが出来ます。 通過算(すれ違い)の公式 すれ違いの時間 = 2つの列車の長さの和 ÷ 2つの列車の速さの和 上の問題に当てはめると、 2つの列車の長さの和 = 80m + 100m = 180m 2つの列車の速さの和 = 秒速m + 秒速16m = 秒速36m となるので、 すれ違いの時間 = 180m ÷ 秒速36m で、 答えは 5秒 となります。
Incoming Term: 出会い算 電車,




0 件のコメント:
コメントを投稿